#562 – Electroboom!

[ogden]

I already answered to that specific question - by looping the measurement wire through the core -, but it doesn't prevent it being re-asked repeatedly, just like before.
These people are indeed like broken records. Or maybe you want to hear the answer from Sredni or bsfeechannel? Maybe I'm not qualified?

Yes I was expecting to continue discussion with Sredni or bsfeechannel, not you. As soon as Lewin's followers agree that path-dependency can be proven using multiple windings of measurement wire which are essentially another secondary winding on transformer, I say that same exact phenomena is true in Romer's/Lewin's experiment and there is no such thing as path-dependency. It is just EMF induced in two wire loops! One can connect them such a way that EMF's cancels out - there will be no current flowing, thus 0V reading on voltmeter.

The key difference in Lewin's excercise and ogden's transformer circuit is that the former circuit is completely placed within the varying field, making it impossible to route the probe wires outside of the field.

It was said already - Maxwell-Faraday equation does not care about size/diameter/area of wire loop. Hopefully you agree. It was proven as well. Probe wires in Lewin's experiment are routed *around* varying field, same way as circuit wires. It is fallacy to think that circuit receives EMF in Lewin's experiment, but probe wires miraculously avoid Faraday's Law of Induction. Fact that so many fail to understand such a simple logic is mindboggling. No wonder that most eevblog contributors avoid those threads because they are busy of laughing loud and facepalming.

[thinkfat]

The key difference in Lewin's excercise and ogden's transformer circuit is that the former circuit is completely placed within the varying field, making it impossible to route the probe wires outside of the field. The transformer? The field is contained within the core, and you can conveniently measure from the taps that are bought outside of the field.

Actually, no. The probe wires are all outside of the magnetic flux region in Dr. Lewins experiment.

[Siwastaja]

So many diversions have been discussed that I clearly need to watch the original experiment again, and maybe that would be a good thing to do for everyone else as well, seeing that all questions seem to be about different experiments and different circuits.

[bsfeechannel]

As soon as Lewin's followers agree

I learned electromagnetism in the 1980's long before Lewin's lectures and articles about the subject. We are not here to defend Lewin. We are here to denounce the stupid assertions and outright lies KVLiars make.

that path-directivity can be proven

"Path-directivity", he said.

Man, come on. Stop it. You're not fooling anyone. You don't know the theory, nor the practice, and not even the terminology, because you don't know jack squat what it means.

We've been trying to save you from this embarrassment for quite a few years now. Just don't do it anymore. OK?

[bsfeechannel]

Summarizing a bit:

4) Many people have debunked Lewin's claims, including Mehdi, RDS accademy, and Mabilde.  Neither Jesse nor I are the first ones.

What you didn't say is that Mehdi, RDS, Mabilde and Jesse debunk each other. Mehdi said Lewin measured two different voltages across the same two points of the circuit due to bad probing. Mabilde said it was not bad probing, contradicting Mehdi, but it is because there's a "hidden" EMF in the probes. The RDS guy said the problem is otherwise: the ohm's law, according to him, predicts the presence of a voltage across a static wire that's not the product of its current times its resistance. Contradicting Mehdi and Mabilde. Jesse, the poor bugger, doesn't even have a theory to contradict the others, so he doesn't know what is really at stake, nor what to look for, nor how to interpret the results of his "experiment".

In common, all of the above showed without any doubt that, yes, voltages around a circuit immersed in a varying magnetic field are path-dependent. Jesse's setup even shows that dynamically. He changes the position, i.e. the path, of the hands of his clock and the meter displays a different voltage every time.

If you don't know how to use KVL, it doesn't mean that KVL doesn't work!

No one said KVL doesn't work. Sometimes it works. Sometimes it doesn't. It works when there's no varying magnetic field inside the area delimited by the boundaries of the circuit, and doesn't work otherwise.

[bsfeechannel]

This is incredibly sad. I may have overestimated the EEVBlog forum community quality.

[...]

Now I have realized how mediocre "practical engineers" can be totally manipulated into participating such needless and ridiculous war against science and education. Incredibly sad.

[...]

So get off the high horse and read, read, and reread until you understand. I'm not the only one who did full 180 and needed to apologize. It's not easy.

It's a joy when we finally get it. Things fall into place. But then it's sad, exactly for the same reason.

[ogden]

The key difference in Lewin's excercise and ogden's transformer circuit is that the former circuit is completely placed within the varying field, making it impossible to route the probe wires outside of the field. The transformer? The field is contained within the core, and you can conveniently measure from the taps that are bought outside of the field.

Actually, no. The probe wires are all outside of the magnetic flux region in Dr. Lewins experiment.

Not only probe wires are outside of magnetic flux region of Dr.Lewin's solenoid, but whole test circuit as well. You can do "probes outside of the field" experiment yourself, like this: https://www.eevblog.com/forum/amphour/562-electroboom!/msg3913808/#msg3913808

"Path-directivity", he said.
Man, come on. Stop it. You're not fooling anyone. You don't know the theory, nor the practice, and not even the terminology, because you don't know jack squat what it means.

I am not natural englisch speaker, also you most likely got what I did mean by saying so, but instead of just correcting, you did not miss opportunity to insult, again.

[jesuscf]

Summarizing a bit:

4) Many people have debunked Lewin's claims, including Mehdi, RDS accademy, and Mabilde.  Neither Jesse nor I are the first ones.

What you didn't say is that Mehdi, RDS, Mabilde and Jesse debunk each other. Mehdi said Lewin measured two different voltages across the same two points of the circuit due to bad probing. Mabilde said it was not bad probing, contradicting Mehdi, but it is because there's a "hidden" EMF in the probes. The RDS guy said the problem is otherwise: the ohm's law, according to him, predicts the presence of a voltage across a static wire that's not the product of its current times its resistance. Contradicting Mehdi and Mabilde. Jesse, the poor bugger, doesn't even have a theory to contradict the others, so he doesn't know what is really at stake, nor what to look for, nor how to interpret the results of his "experiment".

In common, all of the above showed without any doubt that, yes, voltages around a circuit immersed in a varying magnetic field are path-dependent. Jesse's setup even shows that dynamically. He changes the position, i.e. the path, of the hands of his clock and the meter displays a different voltage every time.

If you don't know how to use KVL, it doesn't mean that KVL doesn't work!

No one said KVL doesn't work. Sometimes it works. Sometimes it doesn't. It works when there's no varying magnetic field inside the area delimited by the boundaries of the circuit, and doesn't work otherwise.

You are definitively delusional!  Mehdi, Bob Duhamel, Mabilde, Jesse, and I agree without contradiction among other things, that Lewin didn't probe the circuit correctly.  This 'straw man' you are trying to create only highlights your deep ignorance about this subject matter.  Lewin does say KVL doesn't work in the particular experiment that concerns us.  But indeed KVL works as I have demonstrated may times already.

[bsfeechannel]

You are definitively delusional!  Mehdi, Bob Duhamel, Mabilde, Jesse, and I agree without contradiction among other things, that Lewin didn't probe the circuit correctly.  This 'straw man' you are trying to create only highlights your deep ignorance about this subject matter.  Lewin does say KVL doesn't work in the particular experiment that concerns us.  But indeed KVL works as I have demonstrated may times already.

The only thing you agree with is that Lewin is, according to you, wrong, but none of you agree exactly why. And your experiments exhibit exactly the same outcome of Lewin's experiment: it is possible to measure two different voltages at the same time across the same two points of a circuit subjected to a varying magnetic field inside the area delimited by its borders.  In none of your experiments you could measure exactly the same voltage for any position of the probes or the meters.

So ¯\_(ツ)_/¯

[jesuscf]

You are definitively delusional!  Mehdi, Bob Duhamel, Mabilde, Jesse, and I agree without contradiction among other things, that Lewin didn't probe the circuit correctly.  This 'straw man' you are trying to create only highlights your deep ignorance about this subject matter.  Lewin does say KVL doesn't work in the particular experiment that concerns us.  But indeed KVL works as I have demonstrated may times already.

The only thing you agree with is that Lewin is, according to you, wrong, but none of you agree exactly why. And your experiments exhibit exactly the same outcome of Lewin's experiment: it is possible to measure two different voltages at the same time across the same two points of a circuit subjected to a varying magnetic field inside the area delimited by its borders.  In none of your experiments you could measure exactly the same voltage for any position of the probes or the meters.

So ¯\_(ツ)_/¯

Another one for the collection of bsfeechannel's laughable statements!     So, here are some questions for you: 

1) What is the calculated voltage between nodes A and D, V_AD, in Lewin's circuit?

2) Is it the voltage V_AD the same as the voltages measure by the voltmeters in Lewin's circuit?

3) If you are given the measured voltage of the voltmeter as well a the location of the voltmeter's probes in Lewin's circuit, can you determine the correct value of V_AD?

4) If the answer to 3) is yes, how would you do it?

As usual, I expect nothing from bsfeechannel, so if anybody feels like pitching in, go for it.

[bsfeechannel]

I am not natural englisch speaker,

No excuse. You had plenty of time to understand what the path-dependence of voltage means because you have been exposed to this concept for quite a few years now.

also you most likely got what I did mean by saying so

We have corrected you multiple times and you refused to accept the correction. Why would you accept it now?

, but instead of just correcting, you did not miss opportunity to insult, again.

Ignorance is a moral issue. Don't blame me for yours.

[jesuscf]

I am not natural englisch speaker,

No excuse. You had plenty of time to understand what the path-dependence of voltage means because you have been exposed to this concept for quite a few years now.

also you most likely got what I did mean by saying so

We have corrected you multiple times and you refused to accept the correction. Why would you accept it now?

, but instead of just correcting, you did not miss opportunity to insult, again.

Ignorance is a moral issue. Don't blame me for yours.

Look who is talking!  bsfeechannel:  Mr. Laughable ignorance himself!!!  Stop wasting time, calculate the voltage V_AD!

[Siwastaja]

1) What is the calculated voltage between nodes A and D, V_AD, in Lewin's circuit?

We have heard this "question" so many times I think we are reaching a situation which could be considered spam, forbidden by the forum rules. Basically copy-pasting your arguments is not helpful to anyone.

You have been given calculated values many times in this thread, also reasoning behind the numbers. It seems clear you just don't like the answer, or agree with it. Which is fine. But...

Now with sensible adults, discussion goes like this:
1 You ask X
2 You get answered
3 You don't agree
4 You tell why you don't agree so discussion can go on
5a In the end, either you accept being wrong, or you are right. Somebody learns something;
or
5b There is no resolution. End of story. No endless loop. Everybody can go do something else.

Not this:
1 You ask X
2 You get answered
3 You don't agree
4 goto 1, infinitely, word for word. + use the fact that others do not participate in your sick game and copy-paste their answers, as some kind of proof for a victory dance.

I see this as borderline harassment, nothing else. This is not only embarrassing because it's so obvious, but I'm sure everybody feels bad, yourself included, no? Please consider stopping this behavior and start behaving like a decent human being, accepting the fact that you are in disagreement, but trying to go forward.

[ogden]

Ignorance is a moral issue. Don't blame me for yours.

... Said master of ignorance and personal attacks. Why didn't you address other part of my post, claim that everything - probes *and* test circuit are outside of magnetic flux area? Afraid of being cornered same way as with question about 100-turn transformer?

[ogden]

1) What is the calculated voltage between nodes A and D, V_AD, in Lewin's circuit?

We have heard this "question" so many times I think we are reaching a situation which could be considered spam, forbidden by the forum rules. Basically copy-pasting your arguments is not helpful to anyone.

You have been given calculated values many times in this thread, also reasoning behind the numbers. It seems clear you just don't like the answer, or agree with it. Which is fine. But...

Now with sensible adults, discussion goes like this:
1 You ask X
2 You get answered
3 You don't agree
4 You tell why you don't agree so discussion can go on
5a In the end, either you accept being wrong, or you are right. Somebody learns something;
or
5b There is no resolution. End of story. No endless loop. Everybody can go do something else.

Not this:
1 You ask X
2 You get answered
3 You don't agree
4 goto 1, infinitely, word for word. + use the fact that others do not participate in your sick game and copy-paste their answers, as some kind of proof for a victory dance.

I see this as borderline harassment, nothing else. This is not only embarrassing because it's so obvious, but I'm sure everybody feels bad, yourself included, no? Please consider stopping this behavior and start behaving like a decent human being, accepting the fact that you are in disagreement, but trying to go forward.

As you are claiming that this is recursive - you shall not have any difficulties of finding post with answer to this ever repeating question.

[jesuscf]

1) What is the calculated voltage between nodes A and D, V_AD, in Lewin's circuit?

We have heard this "question" so many times I think we are reaching a situation which could be considered spam, forbidden by the forum rules. Basically copy-pasting your arguments is not helpful to anyone.

You have been given calculated values many times in this thread, also reasoning behind the numbers. It seems clear you just don't like the answer, or agree with it. Which is fine. But...

Now with sensible adults, discussion goes like this:
1 You ask X
2 You get answered
3 You don't agree
4 You tell why you don't agree so discussion can go on
5a In the end, either you accept being wrong, or you are right. Somebody learns something;
or
5b There is no resolution. End of story. No endless loop. Everybody can go do something else.

Not this:
1 You ask X
2 You get answered
3 You don't agree
4 goto 1, infinitely, word for word. + use the fact that others do not participate in your sick game and copy-paste their answers, as some kind of proof for a victory dance.

I see this as borderline harassment, nothing else. This is not only embarrassing because it's so obvious, but I'm sure everybody feels bad, yourself included, no? Please consider stopping this behavior and start behaving like a decent human being, accepting the fact that you are in disagreement, but trying to go forward.

Do you know why I keep asking?  Because if you answer it correctly then you'll admit that KVL works in Lewin's circuit, which is the topic of this forum.  So, see if you can calculate V_AD and then measure V_AD and they match...  So start by calculating V_AD first, then we can talk.

[Sredni]

Do you know why I keep asking?  Because if you answer it correctly then you'll admit that KVL works in Lewin's circuit, which is the topic of this forum. 

Ah, yes. The ultimate killer question.

So, see if you can calculate V_AD and then measure V_AD and they match...  So start by calculating V_AD first, then we can talk.

Oh, for Fuchs' sakes!


1) What is the calculated voltage between nodes A and D, VAD, in Lewin's circuit?

It.
Depends.
On.
The.
Path.

Here are a few paths for which VAD, which I call VBA, has the value +0.9V.
Among this paths there are the left circuit branch and the path composed by probes and left voltmeter.



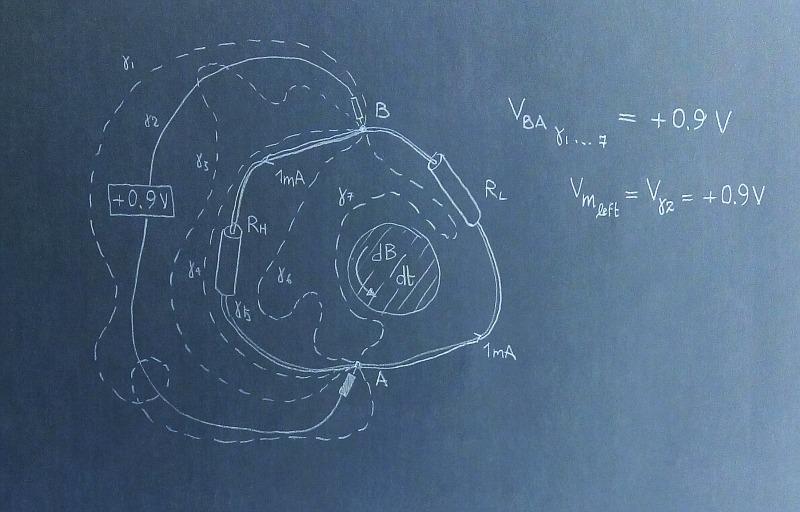
And here are a few paths for which VAD, which I call VBA, assumes the value -0.1V.
Among these paths there are the right circuit branch and the path composed by probes and right voltmeter.



Mind you, my hand was uncertain and I draw a wobbly Lewin circuit, even off center with respect to the EMF generating coil. Still, I can put values on all those voltages, including the voltages across the resistors themselves.
Can you do the same with your KVL-obeying voltages?
Please, do so. Provide the voltages across the resistors and across the probes. Or shut up.

For paths cutting the variable magnetic field region, I can get all values comprised between +0.9V and -0.1V including 0V, 0.5V and 0.4V (what you would call the 'true' voltage in the circular, symmetric and axially aligned Lewin ring - but is it the same in this irregular off-center circuit? You tell me. Or shut up).


2) Is it the voltage VAD the same as the voltages measure by the voltmeters in Lewin's circuit?

Voltage VBA for the left branch of the circuit is the same as the voltage measured by the left voltmeter.
It is also the same as the voltages along paths gamma 1 to 7.
Voltage VBA for the right branch of the circuit is the same as the voltage measured by the right voltmeter.
It is also the same as the voltages along paths gamma 8 to 14.

Here is the total electric field inside the circuit. I am also giving the dimensions of the asymmetric ring. Let's say the inner solenoid perimeter is tangent to the straight line joining A and B and has a diameter of 2 cm. Or, if you prefer, draw the circuit to scale and put your own length.



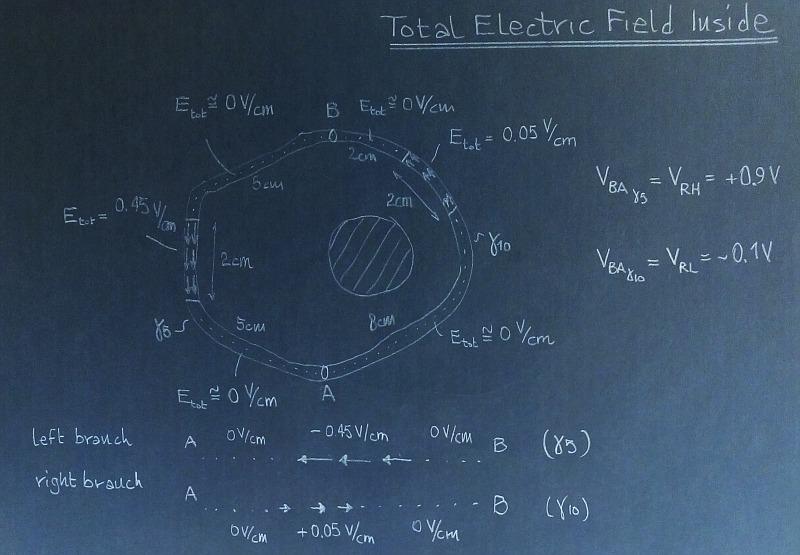
If you feel the total field inside is wrong, by all means provide your solution. Or shut up.

And here is how I compute the voltages along the two branches of circuit from path integrals



I have thrown in, for good measure, the reason why people say KVL no longer works in this circuit: if you sum all voltages along the closed path (be they drops or localized EMFs) you end up with a nonzero total. The total is the EMF linked by the closed path itself. But let's NOT talk about that. Let's focus on the voltages and on how you compute the voltages across the resistors and across the probes for this asymmetric and off-center circuit.
In my world the arcs of conductor and the probes obey Ohm's law and therefore develop no voltage. Put your numbers in, now.

Incidentally, if the segment AB is tangent to the solenoid, VBA along the straight line joining A and B will be 0.9V, in this circuit.


3) If you are given the measured voltage of the voltmeter as well a the location of the voltmeter's probes in Lewin's circuit, can you determine the correct value of VAD?

Yes. But remember:
in my world the voltage depends on the path. So I will be able to tell you what the voltmeter will read and how it relates with the voltages along the left and the right branches of the circuits.


4) If the answer to 3) is yes, how would you do it? 

By applying Faraday's law when my loops include the variable magnetic region, and by applying KVL when they do not.

Now, please, tell me what are the values of the voltages across the resistors and the probes.
We all know we agree on what the voltmeters will measure. Show us how you compute the voltages across the probes and resistors in this asymmetric and off center configuration. Copy the profile of one circuit and report back when you have the results.

EDIT: added missing bold face (pun intended).

[jesuscf]

1) What is the calculated voltage between nodes A and D, VAD, in Lewin's circuit?

It.
Depends.
On.
The.
Path.

Here are a few paths for which VAD, which I call VBA, has the value +0.9V.
Among this paths there are the left circuit branch and the path composed by probes and left voltmeter.

Yes, it depends on the path of the circuit formed by the wires and components.  An unique path that is not changing geometry or moving throughout space. The dashed paths you drew in the figure above are not valid paths because they are incapable of circulating current; they are made of... air?  You can not apply Faraday's law or more generally KVL on those made up paths.  The line integral must follow the circuit.  At this point you are even in conflict with what is correct in Lewin's lectures.  It is a waste of time to argue with you on anything else when you can not grasp this very simple concept.

[Sredni]

Yes, it depends on the path of the circuit formed by the wires and components.  An unique path that is not changing geometry or moving throughout space. The dashed paths you drew in the figure above are not valid paths because they are incapable of circulating current; they are made of... air?  You can not apply Faraday's law or more generally KVL on those made up paths.  The line integral must follow the circuit.  At this point you are even in conflict with what is correct in Lewin's lectures.  It is a waste of time to argue with you on anything else when you can not grasp this very simple concept.

 

Don't let your ignorance of the concept itself of voltage hinder you.
Show us the values for the voltages across the resistors and across the probes in the above asymmetric and offcentered Lewin ring.
All paths are made of copper, resistive material and voltmetrium. All in matter, the way you like.

Now, please, tell us what those values are.
Time to put up or shut up.

[jesuscf]

Yes, it depends on the path of the circuit formed by the wires and components.  An unique path that is not changing geometry or moving throughout space. The dashed paths you drew in the figure above are not valid paths because they are incapable of circulating current; they are made of... air?  You can not apply Faraday's law or more generally KVL on those made up paths.  The line integral must follow the circuit.  At this point you are even in conflict with what is correct in Lewin's lectures.  It is a waste of time to argue with you on anything else when you can not grasp this very simple concept.

 

Don't let your ignorance of the concept itself of voltage hinder you.
Show us the values for the voltages across the resistors and across the probes in the above asymmetric and offcentered Lewin ring.
All paths are made of copper, resistive material and voltmetrium. All in matter, the way you like.

Now, please, tell us what those values are.
Time to put up or shut up.

What you are trying to do here is the good old "moving-the-goalposts" fallacy.  You are trying to distract from the original question; your plan is not going to work.

Back to Lewin's circuit which is perfectly symmetric, with no extra 'dashed' paths.  Let us concentrate on that fixed circuit, with no extra wires of any kind.  If you assume the voltage between nodes A and D, V_AD, is unique at some instant of time (which by the way it is true), can you calculate that voltage?

[ogden]

To prove that "KVL dies", Lewin's cultists suddenly ignore Faraday's law of Electromagnetic Induction they claim to know so well and EMF as such. With same success one can prove that "KVL dies" for simple circuit as chemical battery with load resistor connected. As internal resistance of the battery is so small that can be ignored - we obviously assume it as zero. After all Lewin ignores wire resistance in his experiment as well. Then according to Lewin's approach we use Ohms law to claim that there is no field inside battery, U = IR, but as R=0, then U=0. Then we integrate fields around the circuit to conclude that KVL is for birds

[bsfeechannel]

Back to Lewin's circuit which is perfectly symmetric, with no extra 'dashed' paths.  Let us concentrate on that fixed circuit, with no extra wires of any kind.  If you assume the voltage between nodes A and D, V_AD, is unique at some instant of time (which by the way it is true), can you calculate that voltage?

Before we go back to Lewin's circuit, let's consider friction. You know, friction is a non-conservative force field. Your car consumes fuel basically to overcome friction. Let's suppose that your car makes 10km with 1 liter of fuel. If you want to go from Amarillo, TX, to Santa Fé, NM, you have several options. You can go via Tucumcari and you'll drive 450 km. But if you want to go by way of Raton, NM, it'll take 622 km. If you choose Clovis, NM, it'll be 515 km.

How many liters of fuel you'll need to go from Amarillo to Santa Fé? There's no single correct answer because it depends on the path. Tucumcari: 45 l; Raton: 62.5 l; Clovis: 51.5 l.

So it is with a non-conservative electric field. The energy needed to move a test charge from two points will depend on the path. Since voltage is energy per unit charge, there's where you get your path dependency. That's soooooooo intuitive.

[bsfeechannel]

Lewin's cultists suddenly ignore Faraday's law of Electromagnetic Induction

There are two kinds of people here: those who, in the words of Siwastaja, "get off the high horse and read, read, and reread until you understand", and those who are too lazy to learn electromagnetism and think that attacking those who can teach it will redeem them from their profound stupidity.

[jesuscf]

Lewin's cultists suddenly ignore Faraday's law of Electromagnetic Induction

There are two kinds of people here: those who, in the words of Siwastaja, "get off the high horse and read, read, and reread until you understand", and those who are too lazy to learn electromagnetism and think that attacking those who can teach it will redeem them from their profound stupidity.

Nope!  There is also bsfeechannel, a fine example of the Dunning-Kruger effect.

[bsfeechannel]

Nope!  There is also bsfeechannel, a fine example of the Dunning-Kruger effect.

We both are ignorant, but you don't know it.