-
I just did an energy loss experiment.
I charged an electrolytic capacitor, to 28.9 volts.
I then discharged it to an empty, equal rated, same volts, same farads, capacitor, then read the volts on both at the end,
I made sure I got them the right way around.
it was about 11 point something volts, on both.
that means I lost about 25% of the energy, does this sound right? -
Energy goes with the square of voltage, seems more energy loss, what are the values of the capacitors and what type are them?
-
Thanks for reply, I dont understand what the square of the volts means... to do with energy...
Wouldnt it be if they were both ~14.5 volts each that would be 0% loss?
they are 50 volt.
100 microfarad.
Electrolytic.
I actually want to do it through a spark gap with higher volt caps, then measure the loss through the spark gap after this. -
You should play a bit with this calculator
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/capeng.html
-
So why was it 11 volts on both capacitors, instead of 7 volts?
Isn't the voltage stored on the capacitor how much it is filled?
I didnt use a resistor, maybe I should try it, and check the loss. BRB. -
The energy stored in a capacitor is E = (1/2) CV2.
If your capacitor value for each cap is C, then the initial energy is (1/2) C x (28.9 V)2.
The total energy in both units after connection is (1/2) x (2 C) x (11 V)2.
What is the tolerance on the capacitance values? -
Hmm... Im getting very confused.
When I used the 1k resistor they were 13 volts and 12 volts. but maybe i didnt hold it long enough on.
Its as if it had no effect on energy loss, it just slowed the transfer process down.
I dont know the tolerance, but if you hit the amount of volts, doesnt mean the charge got into the capacitor?
I tested them with an led, and yes it was quite a strong blip on both of them.
Since both capacitors are the same farads, doesnt that take it out of the variables for the experiment? -
Explained here, if you really did that experiment: https://en.wikipedia.org/wiki/Two_capacitor_paradox
-
Im really confused now.

What I'm thinking now, is why did I even lose the 25%???!?!?
Its even one of great paradi, on the internet, amazing... -
Because the paradox is framed with "perfect" components and zero resistance. If you did it with real components, there are other losses.
-
How the hell can an LC oscillator have 99% efficiency (they do ring for a fair amount of time.) when a capacitor loses 25% or 50% when it goes to another capacitor.
How could it be any different than discharging to an inductor?
here: https://www.giangrandi.ch/electronics/ringdownq/ringdownq.shtml
this is clearly more than 75% efficient per rebounce.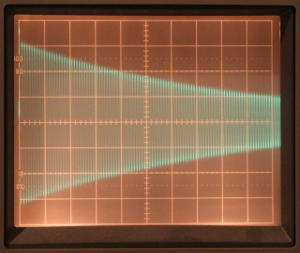
Doesnt this mean if you bounce off an inductor to the next capacitor, you get 98% efficiency or something decent? -
The answer, even in a perfect world with ideal lossless components, is very surprising.
Like the other poster said, the energy in a capacitor is E = (1/2)CV2
Suppose I have a capacitor charged with voltage V, and I connect it through a resistor (R) to another capacitor of the same value with initially no voltage. The total energy in the system before connecting the second capacitor is (1/2)CV2.
At some time, the voltage between the capacitors is the same, and current stops flowing. The energy in the system is then 2 x (1/2)CVT2, where VT is the terminal voltage. There are several ways to figure VT, but here's one. The voltage of the first capacitor will decrease with a time constant of RC/2 (since the two capacitors in series will have a combined capacitance of C/2). So the voltage equation for the first capacitor is V x e-t/(RC/2). The second capacitor will similarly charge with the equation V x (1-e-t/(RC/2)). If you figure out where these two equations are equal, you will find that it is at t=-(RC/2) x ln(1/2), and if you plug that back into the voltage equations, will find that the final voltage is V/2, and is independent of R and C.
So the energy in the system in the final state is 2 x (1/2)(V/2)2 = (1/4)CV2. So we have lost half of our energy. Where did it go? If you do the math, you will find that the energy is disipated in the resistor. But the really crazy thing is (and I encourage you to do the math), as is the final voltage state of the system, it is independent of R. When you are through manipulating the equations, you find that R falls out, and the energy lost is purely a function of V and C. So even if the resistance is zero, the energy is still lost in the resistor.
Try it (calculating the energy lost in the resistor). I=V/R. P=VI. E=integral of P over time. If you do the integration, you will get a result of E=(1/4)CV2 (R drops out of the equation). It's bizzare. -
Explained here, if you really did that experiment: https://en.wikipedia.org/wiki/Two_capacitor_paradox
I hadn't looked at the link before I replied. Interesting. I hadn't run across an explanation of other possible energy loss mechanisms before. I went through the math many years ago when I was curious to know where the energy went. I was surprised at what I found. -
The usual explanation for the zero-resistance case being the same as finite resistance is that there is always inductance in the loop formed by the two capacitors, therefore the circuit will "ring down" as shown in the CRO trace. During that ring-down, the circuit radiates out to the distant galaxies, even if the jumper wire is a superconductor.
Also, since the capacitors are electrolytic, the ESR would be significant, although the system is independent of resistance. -
(apologies rfclown didn't spot your post at first, looks like you had the same explanation)
One thing that may make it clearer, if you take a few different resistances and repeat the experiment, leaving it long enough to settle (or do it in Spice) you will find that as you use progressively smaller resistors, the energy loss stay the same.
From the moment you connect the caps together, with 1k you will have a very small power loss (initial voltage x "low" current) but it lasts a long time as the current flows and the capacitor voltages equalises, at 1 ohm you have a very high initial power loss (initial voltage x "high" current) but it doesn't last very long.. resulting in an equal total energy loss by the time the voltages have fully stabilised. I wouldn't dare speculate where the energy goes.. but I'd always back Kirchhoff in a circuits based problem.
If you mentally extend that to zero ohms between the caps, you have an infinite current flowing for zero time in zero ohms... interestingly if someone wanted (really, really wanted to) to solve the differential equations (properly) I'm about 99% sure (infinity)^2 x 0 x 0 will give the same answer of half the total energy.
Also curiously, the mean energy (total energy of the two capacitors divided by 2) is equal before and after they are connected together... similar to the conservation of momentum in gasses (or many particles bouncing around) where the mean-squared velocity is a useful figure -
whatever you do, dont put a diode, cause then its 0%.

and 2 of the volts didnt even travel, not that I know cause it was 0...
-
.... So even if the resistance is zero, the energy is still lost in the resistor.
 ...
...
Just realized the error in my statement. If R=0, the equations I have for voltage blow up (aren't valid). I recant. If there is any resistance (as in any realistic case), the energy is lost in the resistor. If R=0 I'm not going to try to figure it out now.
I'm not going to try to figure it out now.
-
This was an assignment over 50 years ago in undergrad school. You can solve by integrating the current thru the resistor R connecting the equal valued capacitors from t = 0 to infinity, you find that half the initial energy is lost in R, but independent of R!!
Or the simpler approach is based on conservation of charge where initial charge Q=CV, with two capacitors in parallel the charge divided between both capacitors, so Q=2CVfinal, and Vfinal=Q/2C, or Vfinal=V/2 since V=Q/C. Now the initial energy is simply (CV^2)/2 and the final energy is (C(V/2)^2)/2 + (C(V/2)^2)/2 for both capacitors, or (CV^2)/8 + (CV^2)/8, or [(CV^2)/2]/2. Thus half the initial energy (CV^2)/2 is lost regardless of method of connecting the two capacitors; Cu wires, carbon resistors, superconducting nanotubes, niobium, YBCO, or BSCCO wires, or whatever you wish to connect the capacitors together with!!
Best, -
The differential equation approach is a little more complicated, but straight forward, so here goes without Google help (like the charge model above, no Google help).
The two caps C are connected by resistor R, thus the current flows thru R and the caps C are now in series, not parallel wrt the current (very important point!!). A little elementary differential equations and calculus will show the current behaves as I(t) = (V/R)e^(-t/tau), where tau is the time constant. Since the capacitors are in series, then tau = R(C/2), thus I(t) = (V/R)e^(-2t/RC).
So the lose in R is the integral of R(I^2) from 0 to infinity:
the integral of R(V/R)^2 (e^2(-2t/RC)) or
integral (V^2/R)(e^(-4t/RC)) evaluated from t=0 to infinity is,
(V^2/R)(-RC/4)[e^(-infinity)- e^(-0)]
or (CV^2)/4
Since the initial energy is (CV^2)/2, then half the initial energy is lost, independent of R. Same result you get with charge conservation as it should be.
Best,
-
Im really confused now.

What I'm thinking now, is why did I even lose the 25%???!?!?
Its even one of great paradi, on the internet, amazing...
I understand, I had a look at some articles on the internet and explanations are often not very clear for me.
First of all there is no paradox from the energy consideration standpoint alone. Since W=1/2Q^2/C, transferring a charge Q from a small to a big capacitance (here C -> two C in parallel hence C->2C) will yield some energy, in other words, since energy is conserved the charge flow will necessarily do some work in the process. It is the same as if you were transferring water from a small to a big tank: if the water level in the final state is lower than in the initial state then the energy of the system decreases and the excess energy must be released in one way or another (mechanical work, dissipation as heat etc.).
A paradox arises ONLY when trying to model the process solely using lossless discrete components so that there is no way the work done by the charge can be accounted for within the model. For me talking about losses by radiation etc. is pointless and confusing even more without this being stated, in the first place. -
Efficiency is always 50%. Loss happens in all system resistances. Energy loss depends only on capacitance and voltage difference. Amount of resistance only defines the time constant. When R approaches 0, t approaches 0 and P approaches infinity.
From practical engineering viewpoint, the problem is what could be called linear regulation; due to voltage mismatch, excess voltage is burned away in resistances because there is no power conversion step like a DC/DC converter. This is pretty obvious if you allow yourself to draw a discrete resistor, then run time-step analysis on pen&paper, for example dividing the charging event to ten timesteps, doing normal Kirchoff stuff to calculate current and voltages, and energy stored in capacitors.
Initially, when one capacitor is at empty and another at full voltage, loss is 100%.
Finally, when the capacitors are at nearly equal in voltage, loss is nearly 0%.
Average loss is 50%.
DC/DC converters solve this problem for example by storing energy in the magnetic field of an inductor so that the same energy can be released at different voltage.
Some people completely "shut down" at this problem, some of them start an infinite forum shitstorm as a psychological reaction to their brain not accepting this. -
Initially, when one capacitor is at empty and another at full voltage, loss is 100%.
50% -
Q is conserved. Q=CV . After charging to Q coulombs the first capacitor has V volts on it. The charge it holds is CV. Connecting the second capacitor distributes the charge between them- the voltage drops. Assuming that the second capcitor has no reisdual charge, and the capacitors are identical, the voltage will be: V= Q/(C1+C2). But its unlikely that the two electolytic capacitors have exactly the same C so the expected and acutal voltages differ. Power losses are I.IR come from the capacitors internal resistance. Arcs and sparks also consume energy from the circuit. Q is lost so energy is lost. The total enrgy in the system is determined by the total charge. Energy is accordingy conserved. E=QV/2
-
This assumption of charge conservation is key to the calculations. It should hold unless there is parallel resistance (leakage) across one or both capacitors. Of course, electrolytics have more leakage than film capacitors. Energy is dissipated in series resistance, but charge is not lost thereby.
-
Analogy. Two cars collide and stick together. Car 1 goes 10 mph and car 2 0 mph. After collision both going 5 mph by conservation of momentum. But only half the original kinetic energy (1/2 mv^2). This is an inelastic collision. In an elastic collision car 1 stops and car 2 goes 10 mph. This would happen if a giant spring were between them. You can see this if you strike one coin with another or even a row of coins where only last coin moves after the collision.
Cars: p=mv E= 1/2 mv^2
Capacitors: Q=CV E= 1/2 CV^2